対角化と支配する

このところ、対角化についての細かい議論を銅蟲さんと続けていました。そもそもどういった状態をもって急増加関数での近似としているのかが正しく掴めていなかったので、様々な事例を追っていたというところです。

銅蟲さんが \(F_3\) の定義を書き下して丁寧な理解をしようとしていたところから話が始まっていますが、いまいち本質的な理解に到達できず、一時期はもっと簡単な形にした s(n)変換で検証を試みようとしていたようで、本人がその一部をアップロードしています。この後、第一クロちゃん数について、近似についての議論があり、4 月 4 日に銅蟲さんの家で開催した「巨大数の土曜日」でやっと考えがまとまりました。

結論から言いますと、支配する（dominates）という考え方をしっかり掴み切れていなかったこのが問題でした。

ここで、巨大数スレにおける操作の対角化について、『巨大数論』の記述を元に、簡単な例を挙げます。例えばハイパー演算子を、Wikipedia における記法を用いて

\begin{array}{l} a^{(0)}b &= b + 1 \\ a^{(1)}b &= a + b \\ a^{(2)}b &= ab \\ a^{(3)}b &= a \uparrow b \\ a^{(4)}b &= a \uparrow\uparrow b \\ &\vdots \\ a^{(n)}b &= \underbrace{a^{(n-1)}a^{(n-1)} \cdots ^{(n-1)}a}_b \end{array}

とし、以下のような表を書くことができます。

\begin{array}{l} x^{(0)}x:& \boldsymbol{1^{(0)}1} ,& 2^{(0)}2 ,& 3^{(0)}3 ,& 4^{(0)}4 ,& \cdots ,& n^{(0)}n \\ x^{(1)}x:& 1^{(1)}1 ,& \boldsymbol{2^{(1)}2} ,& 3^{(1)}3 ,& 4^{(1)}4 ,& \cdots ,& n^{(1)}n \\ x^{(2)}x:& 1^{(2)}1 ,& 2^{(2)}2 ,& \boldsymbol{3^{(2)}3} ,& 4^{(2)}4 ,& \cdots ,& n^{(2)}n \\ x^{(3)}x:& 1^{(3)}1 ,& 2^{(3)}2 ,& 3^{(3)}3 ,& \boldsymbol{4^{(3)}4} ,& \cdots ,& n^{(3)}n \\ & & & & & \ddots & \\ x^{(n)}x:& 1^{(n)}1 ,& 2^{(n)}2 ,& 3^{(n)}3 ,& 4^{(n)}4 ,& \cdots ,& \boldsymbol{(n+1)^{(n)}(n+1)} \end{array}

この表を右方向に進むならば、ハイパー演算子による演算の対象となる数 \(a\) と \(b\) がそれぞれ大きくなりますが、下方向に進むならば、ハイパー演算子の強さ \(n\) が大きくなります。

ここで、先日のブログエントリでも触れた『数学基礎論講義』から「支配する」という概念について、その定義を引用します。

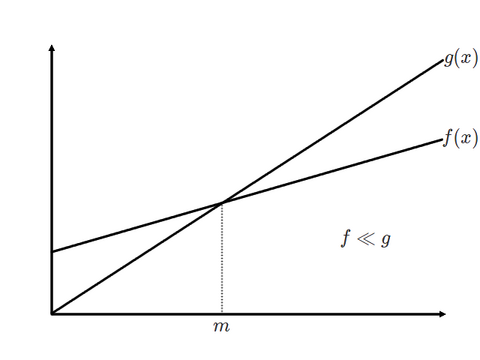
自然数上の 1 変数関数 \(f, g\) に対して，ある \(m\) があって，\(m \lt x\) ならば \(f(x) \lt g(x)\) が成り立つとき，\(g\) は \(f\) を支配するといい \(f \ll g\) と書く．これは \(g\) が \(f\) よりも急増加することを意味している（図 10.7）．

図 10.7

画像は再現したものを GIMP で作成しました。見たままですね。

先程の表の話に戻ります。\(x^{(1)}x\) の増加速度に \(x^{(0)}x\) が追い付くことはできません。これはグラフを書かずとも自明です。すなわち、\(f_1(x) = x^{(1)}x\) は \(f_0(x) = x^{(0)}x\) を支配しています。同様に、\(f_2(x) = x^{(2)}x\) は \(f_1(x) = x^{(1)}x\) を支配しており、これを一般化すると、\(f_{n+1}(x) = x^{(n+1)}x\) は \(f_n(x) = x^{(n)}x\) を支配している、ということになります。

ここまでは原始帰納関数です。原始帰納関数の定義を『巨大数論』から引用します。

原始帰納関数とは、定義域と値域が非負整数である非負整数個の引数をとる関数で、引数に対し、

1. ゼロ関数 (zero function): \(f(x_1, \cdots, x_n) = 0\)
2. 後者関数 (successor function): \(f(x) = x + 1\)
3. 射影関数 (projection function): 複数の引数を持つ関数から、i 番目の引数を返す関数
   \(f(x_1, \cdots, x_n) = x_i\)
4. 合成作用素 (composition operator): f と g の合成関数 h
   \(h(x_1, \cdots, x_m) = f(g_1(x_1, \cdots, x_n), \cdots, g_k(x_1, \cdots ,x_n))\)
5. 原始帰納作用素 (primitive recursion operator): f と g の原始帰納関数 h
   \(h(0, x_1, \cdots, x_k) = f(x_1, \cdots, x_k),\)
   \(h(n + 1, x_1, \cdots, x_k) = g(h(n, x_1, \cdots, x_k), n, x_1 \cdots, x_k)\)

以上の３つの関数と２つの作用素（操作）を有限回適用した関数である。

ここで重要なのは、原始帰納作用素で繰り返し回数を意味している \(n\) が定数であることです。定数回の繰り返しであるということは、\(n\) を増やすだけでより強い演算子となってそれまでの関数を支配できてしまいます。そこで、先程の表において太字にしてあるところだけに着目すると、\(g(x) = x^{(x-1)}x\) となり、演算子の強さそのものが変数化しています。これにより、任意の \(n\) に対し \(f_n(x) = x^{(n)}x\) を定義しても、\(g(x) = x^{(x-1)}x\) はそれを支配します。\(x\) に与える数が充分に大きれば、演算子がより強くなってしまうためです。すなわち、任意の \(n\) に対し、ある \(m\) が存在し、\(x > m\) の時に \(g \gg f_n\) となります。

つまり、ハイパー演算子は、関数に対し定数回の繰り返ししかできないあらゆる原始帰納関数を支配しています。これが 2 重帰納関数です。また、先程の表で斜めに配置した太字の部分を拾い上げていくことを、巨大数スレでは「操作の対角化」と呼んでいたそうです。この対角化は 2 次元的なものであり、3 次元的に発展させることもできます。\(F_1\) は 3 次元での対角化を行う、3 重帰納関数を定義しています。\(F_5\) 読解エントリではこの考えを推し進めた「n 次元の対角化」、次元の数が変数化された「超次元」、「n 超次元での対角化」や、それを更に超えた次元に言及しています。\(F_5\) の凄まじさがわかりますね。

このエントリでは、表の見た目のわかりやすさを重視するためにハイパー演算子を使いましたが、『巨大数論』ではアッカーマン関数の漸化式から、関数の羃の形にすることで、数え上げを用いて説明しています。ところで、この数え上げって元々は離散数学における概念でしょうか。

対角化と支配することについてまとまったので、とりあえず投稿しておきます。ここから急増加関数、s(n)変換、第一クロちゃん数とその近似の話をしなければならないのですが、力尽きたのでエントリを分けます。また、カリー化を使ってハイパー演算子を関数の羃の形にして数え上げの話まで含めようとしたのですが、支配することの理解に本質的な話ではないこと、またちょっと手法に無理があることから途中放棄しています。しかしカリー化は理解しておくに足る概念であるため、後でそれはそれとして書いておきます。

ところで最後に書いておきますが、支配することの定義から自明なように、関数の引数は \(x\) とだけしてあればよく、そこをいじる必要はありません。現時点において、フカシギの数え方に \(f_2(n^2)\) という近似がありますが、こういったものは美しくない答えを避けるという考えからすると、改善の余地があるものと思います。そもそも関数そのものが操作を行うものであり、この形では引数部分で操作が発生してしまいますから、そこにも問題があります。

ではまた。

追記: 続きである User_blog:Limitofempty/急増加関数とs(n)変換 を書き終えました。