Poly-cell notation is a notation invented by Sbiis Saibian when he was in 2nd grade.[1] It is an early ancestor of the more powerful Hyper-E notation, which operates on a similar basis.
Stack notation[]
Stack notation is an extension of scientific notation. It is a triadic operator consisting of three arguments: a base, a replicator, and a determinant. The replicator is a nonnegative integer; the base and the determinant can be any real numbers, but they must be nonnegative integers in further extensions to the notation.

1010...10303,
with 10 copies of 10.
The base is drawn inside a square, followed by the replicator in a rectangle, and the determinant inside a triangle, as shown in the image. In plaintext, it is represented by [b][r]<d>.
- Definition
- [b] is a square.
- [r](in the second) is a rectangle.
- <d> is a triangle.
The notation is defined recursively with the following rules:
- [b][0]<d> = d. When r is zero, there is no b, so there is only d.
- [b][r + 1]<d> = b[b][r]<d>
In other words, [b][r]<d> = bb...bd with r copies of b (including the base b). This is equivalent to E(b)d#r in hyper-E notation.
Examples:
- [2][2]<3> = 223 = 28 = 256
- [2][3]<3> = 2223 = 1.1579208924... × 1077
- [10][1]<6> = million
- [10][1]<100> = googol
- [10][1]<303> = centillion
- [10][2]<10> or [10][3]<1> = trialogue
- [10][2]<100> = googolplex
- [10][10]<1> = decker
- [10][10]<303> = 1010...10303 with 10 copies of 10
- [10][100]<1> = giggol
- [10][100]<100> = grangol
- [3][327]<1> = tritri
Stack notation exhibits tetrational growth with respect to the replicator.
Diamond notation[]
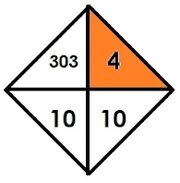
Diamond notation is an extension to stack notation created by nesting stack notation within itself. A second replicator r2 is introduced to indicate the depth of this stack. For the notation, a square is rotated 45 degrees partitioned into four cells in which the four arguments are placed in reading order: d, r2, r, b.
In ASCII, this is written as
- /d|r2\
- \r|b/.
Inline, this is written "a d, r2, r, b diamond."
It is recursively defined by the following:
- d, 0, r, b diamond = r
- d, r2 + 1, r, b diamond = [b][d, r2, r, b diamond]<d>
Examples[]
/303| 1\
\10 |10/ = [10][10]<303>
/303| 2\
\10 |10/ = [10][ [10][10]<303> ]<303>
/303| 3\
\10 |10/ = [10][ [10][[10][10]<303>]<303> ]<303>
This notation exhibits pentational growth with respect to the second replicator.
5-cells and beyond[]
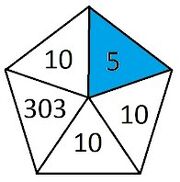
<5|10|10|303|10> = <<4|10|10|303|10>|10|10|303|10>
In 5-cell notation, the third replicator determines the number of "2nd replicator embeddings" in diamond notation and has hexational growth.
In 6-cell notation, the fourth replicator determines the number of "3rd replicator embeddings" in 5-cell notation and has heptational growth.
And in general, n-cell notation can determine number of "(n-3)-th replicator embeddings" in (n-1)-cell notation and has (n+1)-ational growth.

Poly-cell notations (poly-cell hierarchy)
