对数列系统

对数列数 是一个巨大的数字，Bashicu ^[1]于2014年设计^[2]并于2018年更新^[3]，它是关于\(f_{\vartheta(\Omega_\omega）+1}(10)\)大小。 ^[4]^[5]该算法称为对数列系统。该程序是 Bashicu 原始数列系统程序的扩展。

该对数列是非负整数对的有限长度序列，例如 (0,0)(1,1)(2,2)(3,3)(3,2) 对数列 \(P\) 作为从自然数 \(n\) 到自然数 \(P[n]\) 的函数，例如 (0,0)(1,1)(2,2)(3,3)(3,2)[n] 写。假设函数 P[n] 近似于 Hardie层次的增长率，订单号是 \(\alpha\)，对数列 P 让它代表序数\(\alpha\)。也就是说，它可以写成 \((0,0)(1,1)(2,2)(3,3)(3,2)=\psi(\psi_1(\Omega_2))\)。

我们目前正在验证 Bashicu矩阵系统，它是对数列系统的扩展。虽然对序列是由程序定义的，但它类似地由basicu矩阵系统的 2 行矩阵定义。

定义[]

原始定义用大数搜索吧10编写，如下所示：

（原始定义：发表于大数搜索吧于2014年8月18日）

dim A(Infinity):dim B(Infinity):C=9
for D=0 to 9
  for E=0 to C
    A(E)=E:B(E)=E
  next
  for F=C to 0 step -1
    C=C*C
    if B(F)=0 then G=1 else G=0
    for H=0 to F*G
      if A(F-H)<A(F) or A(F)=0 then I=H:H=F*G
    next
    for J=1 to C*G*I
      A(F)=A(F-I):B(F)=B(F-I):F=F+1
    next
    G=1-G
    for K=1 to F*G
      if A(F-K)<A(F) and B(F-K)<B(F) then L=A(F)-A(F-K):M=K:K=F*G
    next
    for N=1 to C*G*M
      A(F)=A(F-M)+L:B(F)=B(F-M):F=F+1
    next
  next
next
print C

（更正后：作者本人于2018年5月26日更新，计算内容与原始版本不同）

dim A[∞],B[∞]:C=9
for D=0 to 9
 for E=0 to C
  A[E]=E:B[E]=E
 next
 for F=C to 0 step -1
  C=C*C
  for G=0 to F
   if A[F]=0 | A[F-G]<A[F]-H  then
    if B[F]=0 then 
     I=G:G=F
    else
     H=A[F]-A[F-G]
     if B[F-G]<B[F] then I=G:G=F
    endif
   endif
  next
  for J=1 to C*I
   A[F]=A[F-I]+H:B[F]=B[F-I]:F=F+1
  next
  H=0
 next
next
print C

从 for D=0 to 9 到 next 循环计算\(C=f_{\vartheta(\Omega_\omega)}(C)\)，并通过重复此计算10次来计算对数 \(f_{\vartheta(\Omega_\omega)+1}(10)\)。

创建该程序的目的是根据 Bignum Bakeoff 大赛的规则，减少字符数。 278个字符，不包括空格和换行代码。

#define A a[f]
#define B b[f]
 #define M = malloc(9),
#define W while (
main(f) {
   int *a M *b M c = 9, d = 10, h, i, k;
   W d--) {
       f = h = c + 1;
      W h--) a[h] = b[h] = h;
      W f--) {
          c *= c;
         h = f + 1;
         W h--)
             (a[h] < A && (b[h] < B || !B) || A + B == 0)?
            (k = B ? A - a[h]: 0, i = f - h, h = 0): 0;
         h = f + c * i; a = realloc(a, h); b = realloc(b, h);
         W f < h) A = a[f-i] + k, B = b[f-i], f++;
      }
    }
    return c;
 }

数学的定义[]

如果您将对数列数作为公式编写，它将如下所示^[6]。

\begin{eqnarray*} \mathrm{大数:}~K&=&\mathrm{Pair}^{10}(9)\\ \mathrm{大函数:}~\mathrm{Pair}(n)&=&\mathrm{expand}\left((0,0)(1,1)\cdots (n+1,n+1)[n]\right)\\ \mathrm{扩充规则:}~\mathrm{expand}([n])&=&n\\ \mathrm{expand}({\boldsymbol S}[n])&=&\left\{\begin{array}{ll} \mathrm{expand}((S_{00},S_{01})\cdots(S_{(X-2)0},S_{(X-2)1})[f(n)])&(\mathrm{if}~/forall yS_{(X-1)y}=0) \\ \mathrm{expand}({\boldsymbol G}{\boldsymbol B}^{(0)}{\boldsymbol B}^{(1)}{\boldsymbol B}^{(2)} \cdots {\boldsymbol B}^{(f(n))}[f(n)])&(\mathrm{otherwise}) \end{array}\right.\\ \mathrm{激活函数:}~f(n)&=&n^2\\ \mathrm{对数列:}~{\boldsymbol S}&=&(S_{00},S_{01})(S_{10},S_{11})\cdots (S_{(X-1)0},S_{(X-1)1})\\ \mathrm{好的部分:}~{\boldsymbol G}&=&(S_{00},S_{01})(S_{10},S_{11})\cdots (S_{(r-1)0},S_{(r-1)1})\\ \mathrm{坏的部分:}~{\boldsymbol B}^{(a)}&=&(B_{00}^{(a)},B_{01}^{(a)})(B_{10}^{(a)},B_{11}^{(a)})\cdots (B_{(X-2-r)0}^{(a)},B_{(X-2-r)1}^{(a)})\\ B_{x0}^{(a)}&=&\left\{\begin{array}{ll} S_{(r+x)0}+a(S_{(X-1)0}-S_{r0})&~(S_{(X-1)1}\gt 0)\\ S_{(r+x)0} &~(\mathrm{otherwise})\\ \end{array}\right.\\ B_{x1}^{(a)}&=&S_{(r+x)1}\\ \mathrm{Bad~root:}~r &=& \left\{\begin{array}{ll} P_1(X-1) & (S_{(X-1)1} \neq 0)\\ P_0(X-1) & (\mathrm{otherwise}) \end{array}\right.\\ S_{x1}~\mathrm{的亲}:~P_1(x)&=&\max\{p|p\lt x \land S_{p1} \lt S_{x1} \land \exists a( p=(P_0)^a(x))\}\\ S_{x0}~\mathrm{的亲}:~P_0(x)&=&\max\{p|p\lt x \land S_{p0} \lt S_{x0} \}\\ \end{eqnarray*}

Bashicu 矩阵计算机[]

在用于计算Bashicu矩阵系统的 bashicu矩阵计算机中，推广了对数列，可以显示对数列的计算过程。此外，可以从 Bashicu 矩阵计算机的站点下载C语言和 BASIC 程序。

以下是计算示例。这里，在原始算法中， n 的值在每次计算时是平方的，但是在这里，计算n的值而不改变 n=2。

相应的序数[]

最多 \(\epsilon_0\)[]

当第二行为0时，它与原始数列系统相同。那就是、

\begin{array}{ll} (0,0) &=& 1 \\ (0,0)(0,0) &=& 2 \\ (0,0)(0,0)(0,0) &=& 3 \\ (0,0)(1,0) &=& \omega \\ (0,0)(1,0)(0,0)(0,0) &=& \omega+2 \\ (0,0)(1,0)(0,0)(1,0) &=& \omega \cdot 2 \\ (0,0)(1,0)(1,0) &=& \omega^2 \\ (0,0)(1,0)(1,0)(0,0)(1,0) &=& \omega^2+\omega \\ (0,0)(1,0)(2,0) &=& \omega^\omega \\ (0,0)(1,0)(2,0)(3,0) &=& \omega^{\omega^\omega} \\ (0,0)(1,0)(2,0)(3,0)(4,0) &=& \omega^{\omega^{\omega^\omega}} \\ \end{array}

对于(0,0)(1,1)，我们得到以下基本序列：这里，假设\(f(n)=n\)。

\begin{array}{ll} (0,0)(1,1)[1] &=& (0,0)(1,0)[1] \\ (0,0)(1,1)[2] &=& (0,0)(1,0)(2,0)[2] \\ (0,0)(1,1)[3] &=& (0,0)(1,0)(2,0)(3,0)[3] \\ (0,0)(1,1)[4] &=& (0,0)(1,0)(2,0)(3,0)(4,0)[4] \\ \end{array}

即 \(\{\omega, \omega^\omega, \omega^{\omega^\omega}, \omega^{\omega^{\omega^\omega}}, \ldots\}\)。因此，它变成了

\begin{array}{ll} (0,0)(1,1) &=& \epsilon_0 \\ \end{array}

最多 \(\epsilon_1\)[]

接下来，考虑 (0,0)(1,1)(1,0) 、 \[(0,0)(1,1)(1,0)[4] = (0,0)(1,1)(0,0)(1,1)(0,0)(1,1)(0,0)(1,1)(0,0)(1,1)[4]\] 获得以下基本序列。

\begin{array}{ll} (0,0)(1,1) &=& \epsilon_0 \\ (0,0)(1,1)(0,0)(1,1) &=& \epsilon_0 \cdot 2 \\ (0,0)(1,1)(0,0)(1,1)(0,0)(1,1) &=& \epsilon_0 \cdot 3 \\ (0,0)(1,1)(0,0)(1,1)(0,0)(1,1)(0,0)(1,1) &=& \epsilon_0 \cdot 4 \\ (0,0)(1,1)(0,0)(1,1)(0,0)(1,1)(0,0)(1,1)(0,0)(1,1) &=& \epsilon_0 \cdot 5 \\ \end{array}

因此，它变成了 \[(0,0)(1,1)(1,0) = \epsilon_0 \cdot \omega\]

接下来，考虑 (0,0)(1,1)(1,0)(1,0)、 \[(0,0)(1,1)(1,0)(1,0)[2] = (0,0)(1,1)(1,0)(0,0)(1,1)(1,0)(0,0)(1,1)(1,0)[2]\] ，获得以下基本序列。

\begin{array}{ll} (0,0)(1,1)(1,0) &=& \epsilon_0 \cdot \omega \\ (0,0)(1,1)(1,0)(0,0)(1,1)(1,0) &=& \epsilon_0 \cdot \omega \cdot 2 \\ (0,0)(1,1)(1,0)(0,0)(1,1)(1,0)(0,0)(1,1)(1,0) &=& \epsilon_0 \cdot \omega \cdot 3 \\ \end{array} 它变成了 \[(0,0)(1,1)(1,0)(1,0) = \epsilon_0 \cdot \omega^2 \] 因此，通过在数字序列的末尾添加(1,0)，序数乘以 \(\omega\)。接下来，考虑在数字序列的末尾添加 (1,0)(2,0)。

喜欢

\[(0,0)(1,1)(1,0)(2,0)[4] = (0,0)(1,1)(1,0)(1,0)(1,0)(1,0)(1,0)[4]\]

，这对应于将序数乘以 \(\omega^\omega\)，因为有一个基本序列，其中逐个添加(1,0),获得

\[(0,0)(1,1)(1,0)(2,0) = \epsilon_0 \cdot \omega^\omega\]

。接下来，考虑(0,0)(1,1)(1,1)、 \[(0,0)(1,1)(1,1)[4] = (0,0)(1,1)(1,0)(2,1)(2,0)(3,1)(3,0)(4,1)(4,0)(5,1)[4]\] ，获得以下基本序列。

\begin{array}{ll} (0,0)(1,1) &=& \epsilon_0 \\ (0,0)(1,1)(1,0)(2,1) &=& \epsilon_0^2 \\ (0,0)(1,1)(1,0)(2,1)(2,0)(3,1) &=& \epsilon_0^{\epsilon_0} \\ (0,0)(1,1)(1,0)(2,1)(2,0)(3,1)(3,0)(4,1) &=& \epsilon_0^{\epsilon_0^2} \\ (0,0)(1,1)(1,0)(2,1)(2,0)(3,1)(3,0)(4,1)(4,0)(5,1) &=& \epsilon_0^{\epsilon_0^{\epsilon_0}} \\ \end{array} 因此，它变成了 \[(0,0)(1,1)(1,1) = \epsilon_1 = \psi(1) \] 。

最多菲弗曼-舒特序数 = \(\Gamma_0\)[]

以相同的方式，计算如下。 \begin{array}{ll} (0,0)(1,1)(2,0) &=& \epsilon_{\omega} = \psi(\omega) \\ (0,0)(1,1)(2,0)(2,0) &=& \epsilon_{\omega^2} = \psi(\omega^2) \\ (0,0)(1,1)(2,0)(3,0) &=& \epsilon_{\omega^\omega} = \psi(\omega^\omega) \\ (0,0)(1,1)(2,0)(3,1) &=& \epsilon_{\epsilon_0} = \psi(\psi(0)) \\ (0,0)(1,1)(2,0)(3,1)(4,0)(5,1) &=& \epsilon_{\epsilon_{\epsilon_0}} = \psi(\psi(\psi(0))) \\ (0,0)(1,1)(2,1) &=& \zeta_0 = \varphi(2,0) = \psi(\Omega) \\ (0,0)(1,1)(2,1)(1,1) &=& \varepsilon_{\zeta_0+1} \\ (0,0)(1,1)(2,1)(1,1)(2,1) &=& \zeta_1= \varphi(2,1) \\ (0,0)(1,1)(2,1)(2,0) &=& \zeta_\omega = \varphi(2,\omega) \\ (0,0)(1,1)(2,1)(2,1) &=& \eta_0= \varphi(3,0) \\ (0,0)(1,1)(2,1)(2,1)(2,1) &=& \varphi(4,0) \\ (0,0)(1,1)(2,1)(3,0) &=& \varphi(\omega,0) \\ (0,0)(1,1)(2,1)(3,0)(3,0) &=& \varphi(\omega,\omega) = \psi(\Omega^\omega\omega)\\ (0,0)(1,1)(2,1)(3,1) &=& \Gamma_0 = \varphi(1,0,0) = \psi(\Omega^\Omega) \\ \end{array}

这已经超过了 TREE(n)。

最多大韦伯伦序数 = \(\psi(\Omega^{\Omega^\Omega})\)[]

以相同的方式，计算如下。 \begin{array}{ll} (0,0)(1,1)(2,1)(3,1)(1,1) &=& \varepsilon_{\Gamma_0+1} \\ (0,0)(1,1)(2,1)(3,1)(1,1)(2,1) &=& \zeta_{\Gamma_0+1} \\ (0,0)(1,1)(2,1)(3,1)(1,1)(2,1)(3,1) &=& \Gamma_1 = \varphi(1,0,1) \\ (0,0)(1,1)(2,1)(3,1)(2,0) &=& \Gamma_\omega = \varphi(1,0,\omega) \\ (0,0)(1,1)(2,1)(3,1)(2,1) &=& \varphi(1,1,0) \\ (0,0)(1,1)(2,1)(3,1)(2,1)(1,1)(2,1)(3,1)(2,1) &=& \varphi(1,1,1) \\ (0,0)(1,1)(2,1)(3,1)(2,1)(2,0) &=& \varphi(1,1,\omega) \\ (0,0)(1,1)(2,1)(3,1)(2,1)(2,1) &=& \varphi(1,2,0) \\ (0,0)(1,1)(2,1)(3,1)(2,1)(3,1) &=& \varphi(2,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,0) &=& \varphi(\omega,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1) &=& \varphi(1,0,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(1,1)(2,1)(3,1)(3,1) &=& \varphi(1,0,0,1) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(2,1) &=& \varphi(1,0,1,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(2,1)(3,1) &=& \varphi(1,1,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(2,1)(3,1)(2,1)(3,1) &=& \varphi(1,2,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(2,1)(3,1)(3,1) &=& \varphi(2,0,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(2,1)(3,1)(3,1)(2,1)(3,1)(3,1) &=& \varphi(3,0,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(3,0) &=& \varphi(\omega,0,0,0) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(3,1) &=& \varphi(1,0,0,0,0) = \psi(\Omega^{\Omega^3}) \\ (0,0)(1,1)(2,1)(3,1)(3,1)(3,1)(3,1) &=& \varphi(1,0,0,0,0,0) = \psi(\Omega^{\Omega^4}) \\ (0,0)(1,1)(2,1)(3,1)(4,0)&=& \psi(\Omega^{\Omega^\omega}) \text{(小韦伯伦序数)} \\ (0,0)(1,1)(2,1)(3,1)(4,0)(3,1) &=& \psi(\Omega^{\Omega^{\omega+1}}) \\ (0,0)(1,1)(2,1)(3,1)(4,0)(4,0) &=& \psi(\Omega^{\Omega^{\omega^2}}) \\ (0,0)(1,1)(2,1)(3,1)(4,0)(5,0) &=& \psi(\Omega^{\Omega^{\omega^\omega}}) \\ (0,0)(1,1)(2,1)(3,1)(4,0)(5,1) &=& \psi(\Omega^{\Omega^{\varepsilon_0}}) \\ (0,0)(1,1)(2,1)(3,1)(4,1) &=& \psi(\Omega^{\Omega^\Omega}) \text{(大韦伯伦序数)} \end{array}

最多巴克曼霍华德序数 \(\psi(\epsilon_{\Omega+1})\)[]

\begin{array}{ll} (0,0)(1,1)(2,1)(3,1)(4,1)(4,0) &=& \psi(\Omega^{\Omega^{\Omega \cdot \omega}}) \\ (0,0)(1,1)(2,1)(3,1)(4,1)(4,1) &=& \psi(\Omega^{\Omega^{\Omega^2}}) \\ (0,0)(1,1)(2,1)(3,1)(4,1)(5,0) &=& \psi(\Omega^{\Omega^{\Omega^\omega}}) \\ (0,0)(1,1)(2,1)(3,1)(4,1)(5,1) &=& \psi(\Omega^{\Omega^{\Omega^\Omega}}) \\ (0,0)(1,1)(2,1)(3,1)(4,1)(5,1)(6,1) &=& ψ(\Omega^{\Omega^{\Omega^{\Omega^\Omega}}}) \\ (0,0)(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)(7,1) &=& ψ(\Omega^{\Omega^{\Omega^{\Omega^{\Omega^\Omega}}}}) \\ (0,0)(1,1)(2,2) &=& \psi(\epsilon_{\Omega+1}) = \psi(\psi_1(0)) \\ \end{array}

最多 \(\vartheta(\Omega_\omega)\)[]

\begin{array}{ll} (0,0)(1,1)(2,2)(0,0) &=& \psi(\psi_1(0))+1 \\ (0,0)(1,1)(2,2)(1,0) &=& \psi(\psi_1(0)) \omega \\ (0,0)(1,1)(2,2)(2,0) &=& \psi(\psi_1(0) \omega) \\ (0,0)(1,1)(2,2)(3,0) &=& \psi(\psi_1(\omega)) \\ (0,0)(1,1)(2,2)(3,0)(4,0) &=& \psi(\psi_1(\omega^\omega)) \\ (0,0)(1,1)(2,2)(3,0)(4,1) &=& \psi(\psi_1(\psi(0)))=\psi(\psi_1(\epsilon_0)) \\ (0,0)(1,1)(2,2)(3,1) &=& \psi(\psi_1(\Omega)) \\ (0,0)(1,1)(2,2)(3,2) &=& \psi(\psi_1(\Omega_2)) \\ (0,0)(1,1)(2,2)(3,3) &=& \psi(\psi_1(\psi_2(0))) \\ (0,0)(1,1)(2,2)(3,3)(4,4) &=& \psi(\psi_1(\psi_2(\psi_3(0)))) \\ (0,0)(1,1)(2,2)(3,3)...(9,9) &=& \psi(\psi_1(\psi_2(\psi_3(\psi_4(\psi_5(\psi_6(\psi_7(\psi_8(0))))))))) \\ \end{array}

换句话说，如果\(\textrm{Pair}(n) = (0,0)(1,1) \ldots (n,n)[n]\) 是 \[\textrm{Pair}(n) \approx f_{\vartheta(\Omega_\omega)}(n)\] 。序数 \(\vartheta(\Omega_\omega)\) 是 \(\textrm{PTO}(\Pi_1^1{-}\textrm{CA}_0)\)，小于 \(\textrm{PTO}(\Pi_1^1{-}\textrm{CA}{+}\textrm{BI})\)。所以 \(\textrm{SCG}(n)\) 也许超越 \(\textrm{Pair}(n)\)。

终止证明[]

P进大好きbot^[7]定义标准形式的概念（比普通意义上的正常形式更宽），而 Buchholz 的 \(\psi\) 用于证明对序列系统的终止。^[8]

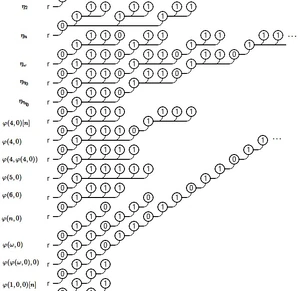
九头蛇表示法[]

Bashicu 显示该对序列由标记的九头蛇(hydra)表示。^[9]

koteitan^[10] 还将 Buchholz 的 hydra (也用标记的 hydra 代表)与一对标记的水印进行了比较。 ^[11]我还创建了一个程序来绘制带有标签的九头蛇^[12]。

源[]

関连项目[]

[1] 作者粉丝账号

[2] 大数搜索吧10: 第一版的定义

[3] 大数搜索吧10: 修改版本定义

[4] 大数搜索吧１０: 计算

[5] 大数论

[6] Purely mathematical definition of BMS

[7] User:P进大好きbot

[8] 用户博客：P进大好きbot/终止对数列

[9] Bashicu 矩阵的解释2

[10] User:Koteitan

[11] 用户博客：koteitan/Bashicu 矩阵的九头蛇符号

[12] 用户博客:Koteitan/对数列系统的九头蛇表示法

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

对数列系统

目录

定义[]

数学的定义[]

Bashicu 矩阵计算机[]

相应的序数[]

最多 \(\epsilon_0\)[]

最多 \(\epsilon_1\)[]

最多菲弗曼-舒特序数 = \(\Gamma_0\)[]

最多大韦伯伦序数 = \(\psi(\Omega^{\Omega^\Omega})\)[]

最多巴克曼霍华德序数 \(\psi(\epsilon_{\Omega+1})\)[]

最多 \(\vartheta(\Omega_\omega)\)[]

终止证明[]

九头蛇表示法[]

源[]

相关链接[]

関连项目[]

Fan Feed

对数列系统

定义[]

数学的定义[]

Bashicu 矩阵计算机[]

相应的序数[]

最多 \(\epsilon_0\)[]

最多 \(\epsilon_1\)[]

最多 菲弗曼-舒特序数 = \(\Gamma_0\)[]

最多 大韦伯伦序数 = \(\psi(\Omega^{\Omega^\Omega})\)[]

最多 巴克曼霍华德序数 \(\psi(\epsilon_{\Omega+1})\)[]

最多 \(\vartheta(\Omega_\omega)\)[]

终止证明[]

九头蛇表示法[]

源[]

相关链接[]

関连项目[]

Fan Feed

最多菲弗曼-舒特序数 = \(\Gamma_0\)[]

最多大韦伯伦序数 = \(\psi(\Omega^{\Omega^\Omega})\)[]

最多巴克曼霍华德序数 \(\psi(\epsilon_{\Omega+1})\)[]